SCEC TPV16/17
TPV16/17 has spontaneous rupture on a vertical, right-lateral, strike-slip fault in a homogeneous half-space with randomly-generated heterogeneous initial stress conditions. The earthquake rupture is artificially nucleated in a circular zone on the fault surface. The rupture then spontaneously propagates outward on the fault surface and encounters heterogeneous stochastic initial stress conditions, some of which prevent it from propagating into certain regions on the fault surface.
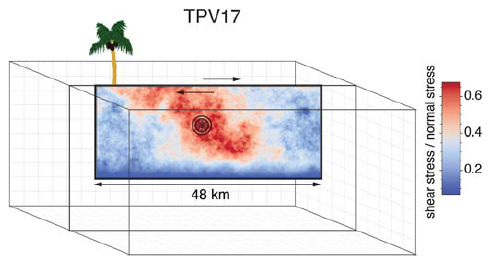
Diagram of TPV16/17. The fault is 40 km long. Colors indicate the ratio of shear stress to normal stress at locations on the fault surface, at the beginning of the simulation.
Geometry
The fault is a vertical, planar, right-lateral, strike-slip fault. The fault reaches the Earth’s surface. Rupture is allowed within a rectangular area measuring 48000 m along-strike and 19500 m down-dip. A node which lies exactly on the border of the 48000 m \(\times\) 19500 m rectangle is considered to be inside the rectangle, and so should be permitted to slip.
The portions of the fault below, to the left of, and to the right of the 48000 m \(\times\) 19500 m rectangle are a strength barrier, within which the fault is not allowed to rupture.
In the example, a vertical fault is generated with Gmsh in Figure [fig:tpv16mesh]. All the files that are needed for the simulation are provided in https://github.com/SeisSol/Examples/tree/master/tpv16.
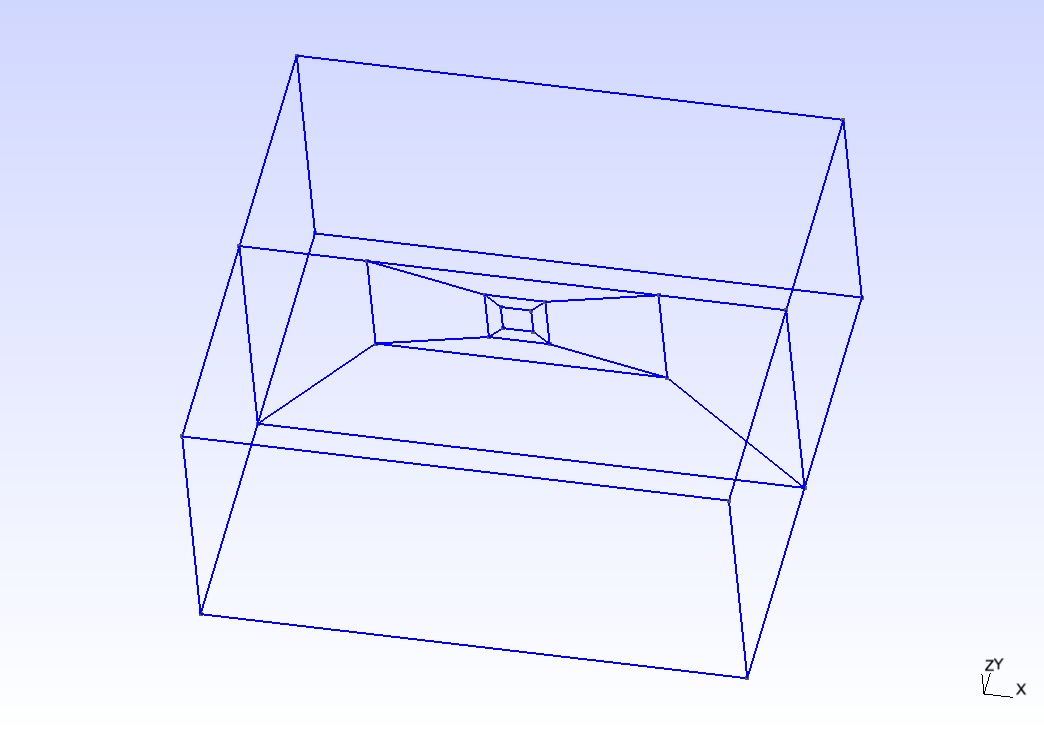
Fault geometry of TPV16. Planar fault with nucleation size of 200 m.
Material parameter
Rock properties are taken to be linear elastic throughout the 3D model volume. The problem description can be found at . Table [table:tpv16material] lists all the material parameters.
Parameter |
Description |
Value |
Unit |
|---|---|---|---|
\(\lambda\) |
Lame’s first parameter |
3.2044e10 |
Pa |
\(\mu\) |
shear module |
3.2038e10 |
Pa |
\(\rho\) |
density |
2670 |
\(kg/m^{3}\) |
\(Q_p\) |
P-wave attenuation |
69.3 |
|
\(Q_s\) |
S-wave attenuation |
155.9 |
|
\(h_{edge}\) |
element edge length |
200 |
m |
Table: Table of bulk and material parameters in TPV16/17.
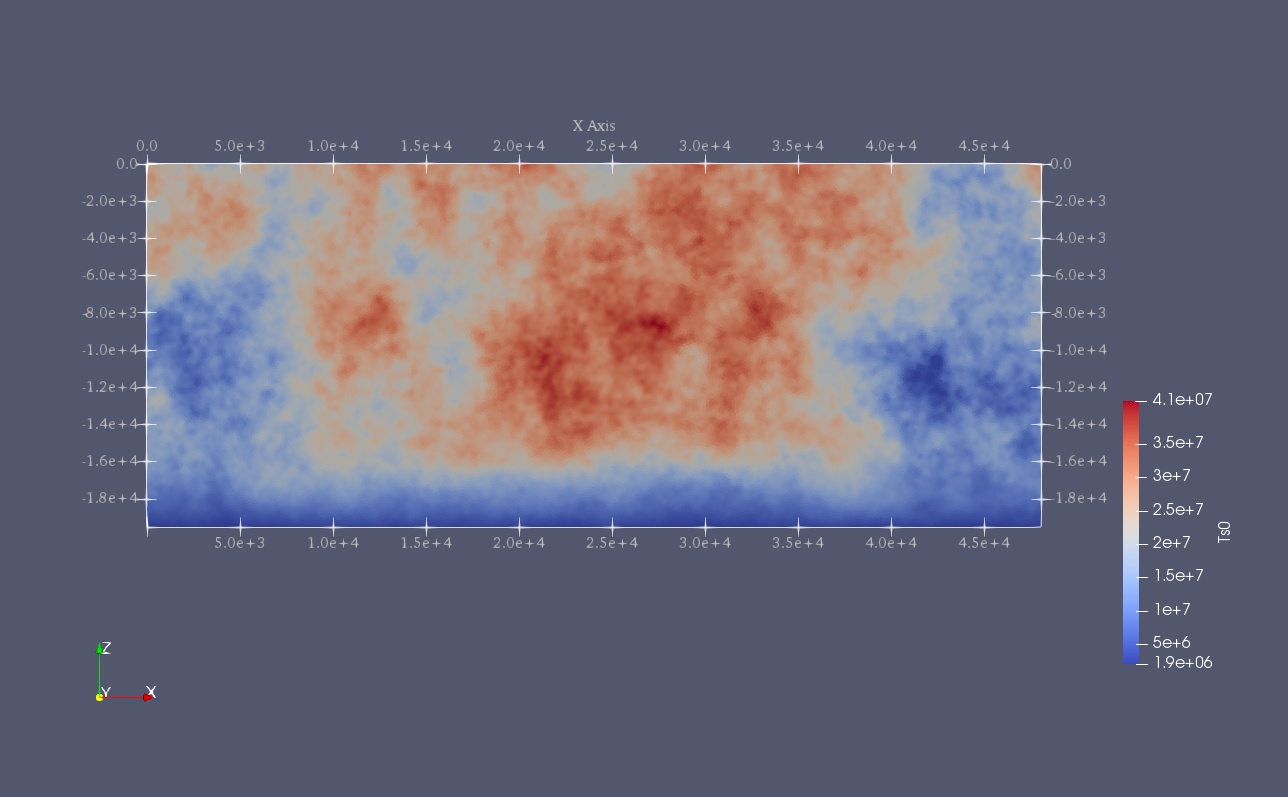
Mapview of fault randomly-generated initial stress in TPV16.
Nucleation parameters
Initial stress (Ts0) is randomly-generated in TPV16/17 (Figure [fig:tpv16ts]).
In TPV16/17, a two-stage nucleation method is used. The first stage is a circular zone of forced rupture which surrounds the hypocenter. Its radius is approximately 1 km (the exact radius is determined as part of the stochastic method that generates the initial stresses). At the hypocenter, the value of then increases with distance from the hypocenter, which creates an expanding circular region of forced rupture. The forced rupture expands at a speed of for 80% of the way, and then for the remaining 20% of the way to the edge of the zone. Outside the zone of forced rupture, is equal to 1.0E9, which means that forced rupture does not occur outside the zone.
The second stage is a circular zone of reduced which surrounds the hypocenter. Its radius is approximately 4 km (the exact radius is determined as part of the stochastic method that generates the initial stresses). In the innermost 10% of the zone, equals 0.04 m. The value of then increases linearly with distance from the hypocenter and reaches its final value of 0.4 m at the edge of the zone. Outside the zone, equals 0.4 m. The effect is to create a circular region of reduced fracture energy surrounding the hypocenter, which helps the rupture to expand during the early part of the simulation.
Results
The earthquake nucleates and the rupture propagates on the fault surface due to the heterogenous stress ratio on the fault. Figure [fig:tpv16slip] shows the fault slip rate along strike-direction at T=5.5 s.
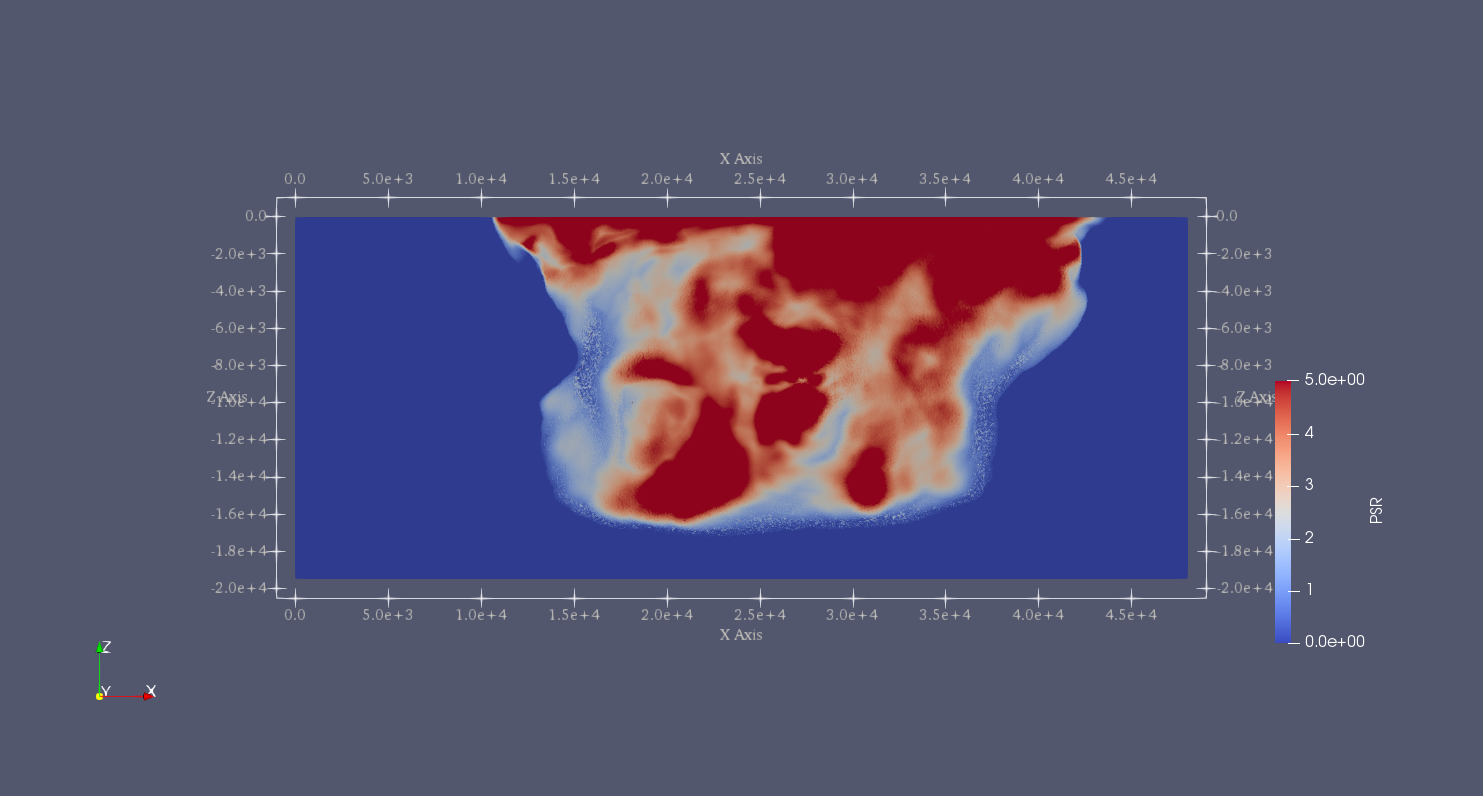
Mapview of fault slip rate along strike-direction.
There are several receivers on the fault surface. Figure [fig:tpv16fault] shows slip rate along the strike- and downdip-direction on the fault at point (15 km, 0 km, -9 km).
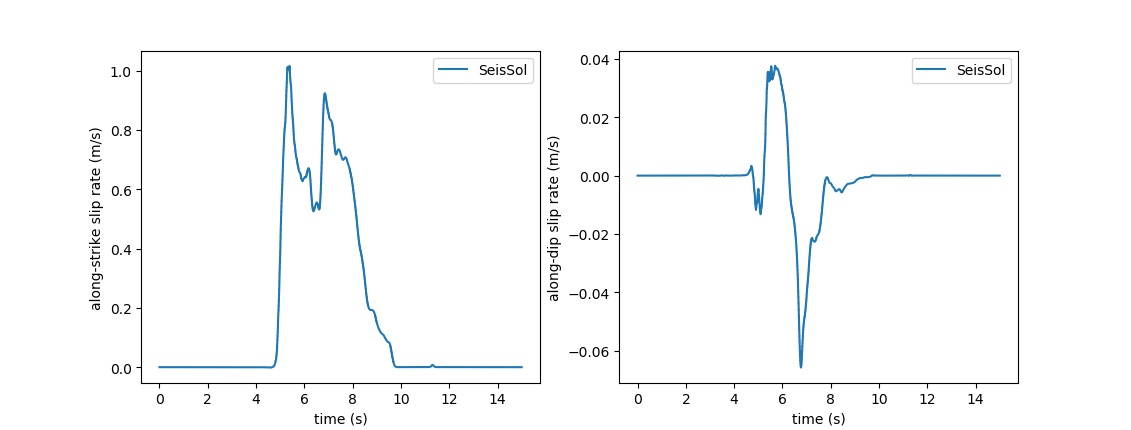
Fault slip along strike- (left)and downdip- (right) direction.

Velocity at two opposite stations across the fault surface.