SCEC TPV12
TPV12 and 13 are verification benchmarks for a 60 degree dipping normal fault embedded in a homogeneous halfspace. The rheology is linear elastic in TPV12 and non-associative Drucker-Prager visco-plastic in TPV13. Initial stress conditions are dependent on depth. Strongly super-shear rupture conditions are assumed.
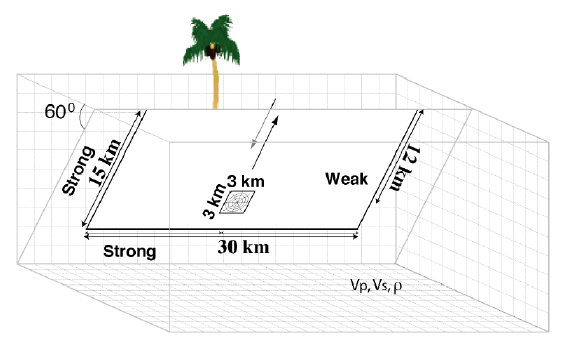
Figure 1: Geometry in SCEC benchmarks TPV12/13, including a 60-degree dipping normal fault.
Geometry
A half-space domain is assumed. The fault is a 60-degree dipping, 30 km \(\times\) 15 km planar, normal fault. It reaches the Earth’s surface, and extends up to 12.99038 km depth. A square nucleation area of 3 \(\times\) 3 km is assumed. In fault coordinates, it is centered at (0, -12) km, that is at a depth of 10.3923 km. The CAD model (see Figure 2) and mesh are generated with Gmsh. All the files that are needed for the simulation are provided here. The geometry and mesh generation process is similar to TPV5.
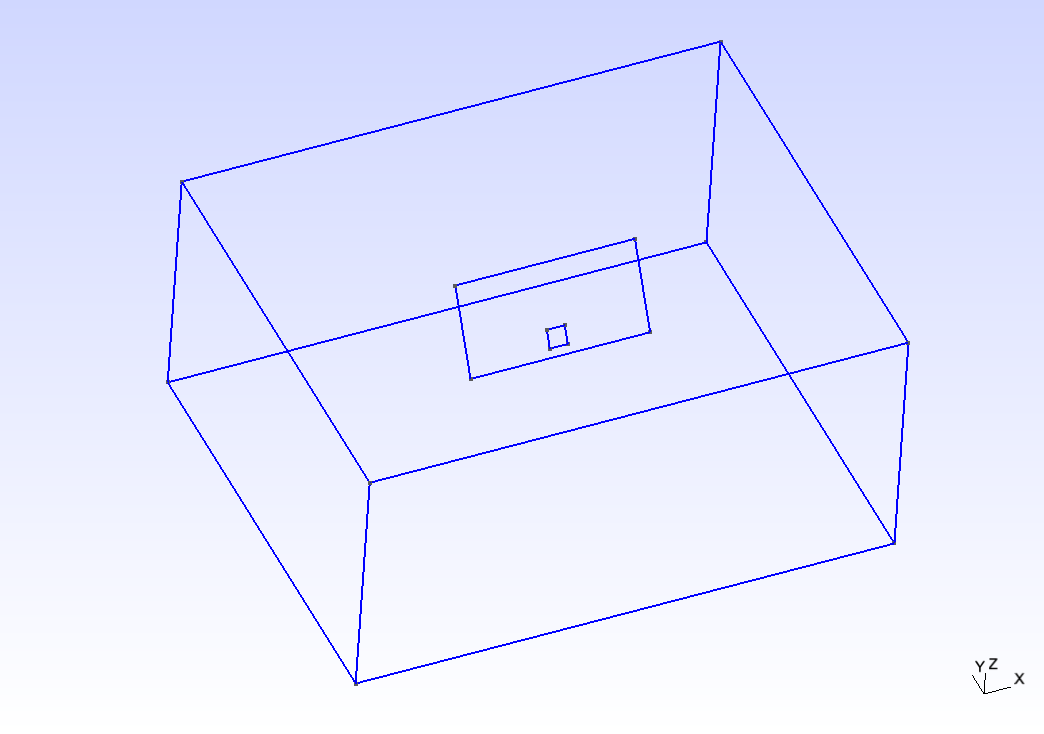
Figure 2: TPV12/13 geometry modeled in Gmsh. The domain box is 500 km \(\times\) 500 km \(\times\) 50 km. The fault reaches the top surface.
Nucleation strategy
In previous benchmarks, nucleation is achieved by imposing higher initial shear stress within the nucleation zone. In TPV12 and TPV13, nucleation is achieved by decreasing the static friction coefficient, leading the initial shear stress to exceed fault strength.
Parameters
friction parameters
TPV12 uses a linear slip weakening law with different parameters inside and outside the nucleation zone. The parameters are listed in the table below:
Parameter |
description |
Value |
Unit |
|---|---|---|---|
d_c |
critical distance |
0.50 |
m |
cohesion |
shear stress cohesion |
-200 000 |
Pa |
inside the nucleation zone |
|||
mu_s |
static friction coefficient |
0.54 |
|
mu_d |
dynamic friction coefficient |
0.10 |
|
outside the nucleation zone |
|||
mu_s |
static friction coefficient |
0.70 |
|
mu_d |
dynamic friction coefficient |
0.10 |
|
Table 1: frictions parameters used in TPV12/13.
Initial stress
The initial stress is assumed depth-dependent in TPV12/13. Above 11951.15 m depth, deviatoric stresses are non-zero, and the stress field is well orientated for rupture of the normal fault. Below, the stress is isotropic.
Parameter |
Value |
|---|---|
above 11951.15 m depth |
|
\(\sigma_1\) |
26460 Pa/m \(\times\) H |
\(\sigma_3\) |
15624.3 Pa/m \(\times\) H |
\(\sigma_2\) |
\((\sigma_1+\sigma_3)/2\) |
\(P_f\) |
\(1000 \mathrm{kg/m}^3 \times 9.8 \mathrm{m/s}^2 \times H\) |
below 11951.15 m depth |
|
\(\sigma_1,\sigma_2,\sigma_3\) |
\(2700 \mathrm{kg/m}^3 \times 9.8 \mathrm{m/s}^2 \times H\) |
Results
SeisSol output can be visualized directly in Paraview by loading their xdmf files.

Figure 3: Fault and volume output of TPV12 visualized in Paraview. Fault slip rate in dip-direction (SRd) and vertical velocity (w) in the volume. A cut-view of the volume output allows visualizing the unstructured tetrahedral mesh.