SCEC TPV13

TPV13 is similar to TPV12 except for the non-associative Drucker-Prager visco-plastic rheology.

The Drucker-Prager yield function is given by:

\(F(\sigma)=\sqrt{J_2(\sigma)}-Y(\sigma)\)

\(Y(\sigma)\) is the Drucker-Prager yield stress, given as:

\(Y(\sigma) =\max(0,c\cos \phi - (\sigma_m +P_f)\sin \phi)\)

with \(\sigma_m = (\sigma_{11}+\sigma_{22}+\sigma_{33})/3\) the mean stress,

\(c\) the bulk cohesion, \(\phi\) the bulk friction and \(P_f\) the fluid pressure (1000 kg/m \(^3\)). In TPV13 benchmark, \(c=\) 5.0e+06 Pa and \(\phi\) =0.85.

\(J_2\) is the second invariant of the stress deviator:

\(J_2(\sigma) = 1/2 \sum_{ij} s_{ij} s_{ji}\)

with \(s_{ij} = \sigma_{ij} - \sigma_m \delta_{ij}\) the deviator stress components.

The yield equation has to be satisfied:

\(F(\sigma)\leq 0\)

When \(F(\sigma) < 0\), the material behaves like a linear isotropic elastic material, with Lame parameters \(\lambda\) and \(\mu\).

Wen \(F(\sigma) = 0\), if the material is subjected to a strain that tends to cause an increase in \(F(\sigma)\), then the material yields and plastic strains accumulates.

Nucleation

TPV13 uses the same nucleation strategy as TPV12.

Plasticity parameters

To turn on plasticity in SeisSol, add the following lines in parameters.par:

&Equations
Plasticity = 1 ! default = 0
Tv = 0.03 ! Plastic relaxation
/

Plasticity related parameters are defined in material.yaml:

!Switch
[rho, mu, lambda, plastCo, bulkFriction]: !ConstantMap
  map:
    rho:                 2700
    mu:           2.9403e+010
    lambda:        2.941e+010
    plastCo:          5.0e+06
    bulkFriction:        0.85
[s_xx, s_yy, s_zz, s_xy, s_yz, s_xz]: !Include tpv12_13_initial_stress.yaml

Results

Figure 1 compares the slip-rates along strike and dip in TPV12 (elastic) and TPV13 (visco-plastic). The peak slip rate in TPV12 is higher than in TPV13. This difference can be attributed to the inelastic response of the off-fault material. See Wollherr et al. (2018) for detailed discussions.

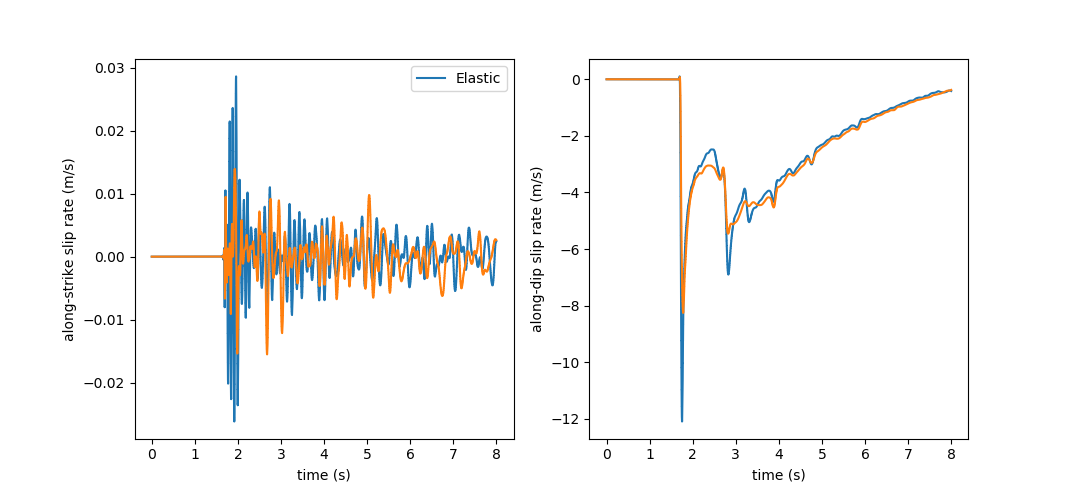
along-strike and along-dip slip rate in TPV12 and 13 — Figure 1: along-strike (left) and along-dip (right) slip rate in TPV12 (blue) and 13 (orange).